Gradient Ascent #10

Graph theory, graph convolutional networks, knowledge graphs

Feb 07, 2021

Welcome to the 10th edition of Gradient Ascent. I’m Albert Azout, a prior entrepreneur and current investor. On a regular basis I encounter interesting scientific research, startups tackling important and difficult problems, and technologies that wow me. I am curious and passionate about machine learning, advanced computing, distributed systems, and dev/data/ml-ops. In this newsletter, I aim to share what I see, what it means, and why it’s important. I hope you enjoy my ramblings!

Is there a founder I should meet?

Send me a note

Want to connect?

Find me on LinkedIn, Angelist, Twitter

Hi everyone! I’m back…

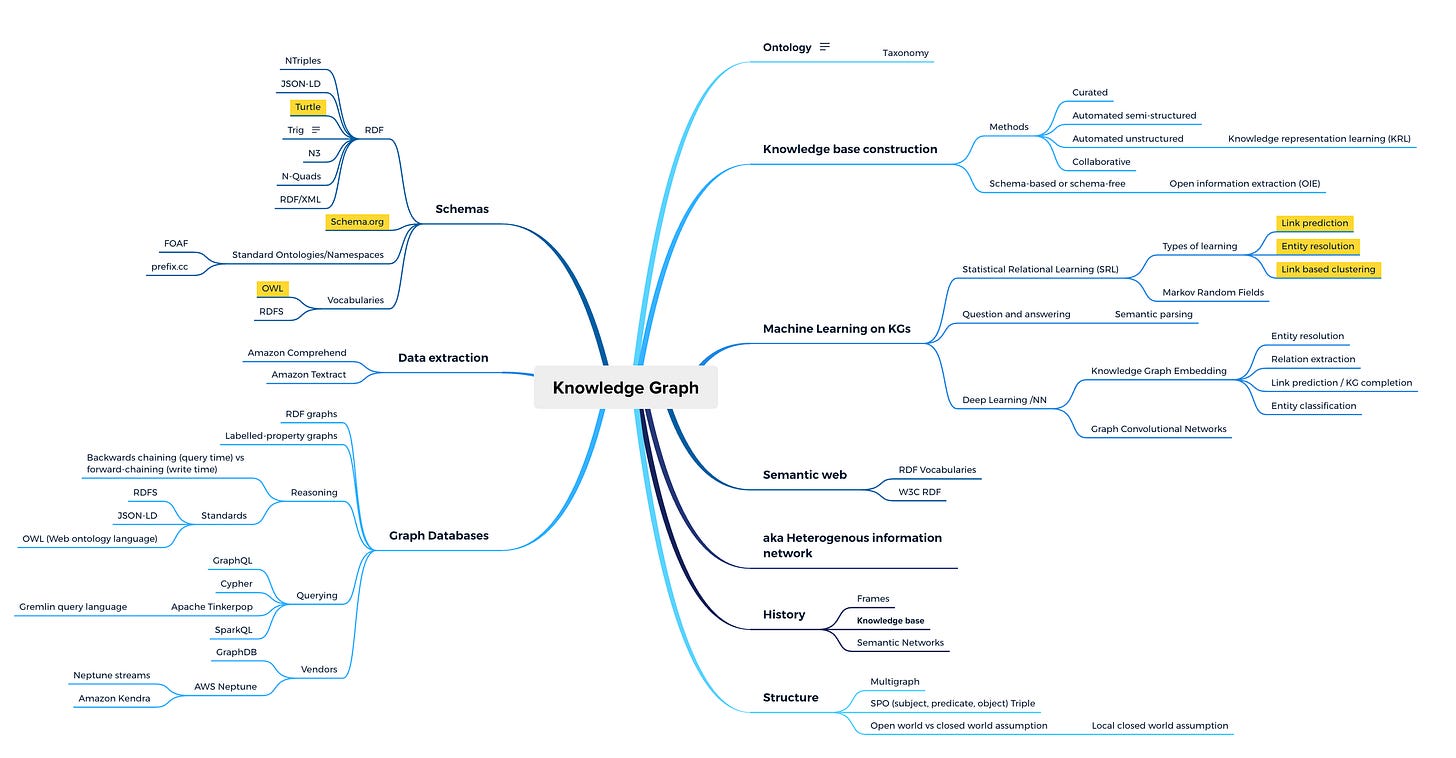
Deep in the bowels of academic research, there is a resurgence of interest in machine learning on graphs, and specifically knowledge graphs. I have spent a several days surveying the latest work (and many years following the topic). A snapshot of my recent taxonomic journey is below:

A majority of the natural data generated in the world can be represented as a graph. Several varieties of graphs exist, including simple undirected graphs with bidirectional edges and vertices, or directed graphs where edges flow in one direction, or heterogenous graphs with varying vertex types or edge types, etc.

Real-world graphs that represent natural phenomena are typically complex networks with non-trivial topologies (i.e. brain neural networks, protein networks, social networks, etc). In fact, complex networks can be represented as directed, multiplex (multi-edge) graphs where nodes and edges co-evolve in time (this is an interesting and dense area of research in itself, with topics like power law degree distributions and scale-free networks ).

Much like traditional machine learning and computer vision evolved from hand-crafted features to statistically learned features, and then to deeper networks with multiple layers of non-linear transformations, graph learning has evolved from traditional graph theoretic approaches to more complex (approximate) message-passing and graph embedding techniques. These methods expand relational inductive biases (like locality and translational invariance in convolutional nets for vision data) to permutation invariance when the inputs to the neural nets are graphs.

At a high level, there are three main problem settings for graph neural networks:

Node/entity classification - classifying nodes into categories based on structural graph (and other) features. Node classification is related to traditional supervised or semi-supervised classification.
Link prediction - Predicting the existence (or future) edges between nodes based on the structural properties of the network.
Community detection - Partitioning the graph into distinct (non-overlapping or loosely overlapping) subgraphs. This is related to unsupervised or semi-supervised clustering.

Modern techniques (mostly) leverage two high-level approaches to solve these problems:

Graph embedding - learning a representation (encoder) of the graph in a lower dimension (typically a vector representation). The graph embedding is used for downstream tasks (i.e. decoder).
Message-passing with specialized graph operators - leverage the graph structure to propagate information between nodes, with some operator which transforms the messages. In neural nets, the parameters of the operator are learned.

An interesting sub-area of research is knowledge graphs (KGs), a specialized graph meant to encode human knowledge. Knowledge graphs express knowledge as a network of facts, where a fact is a (subject, predicate, object) triple (i.e. (Elon Musk, CEO, Tesla)). KGs emerged, historically, from semantic networks which evolved into the semantic web and RDF schemas/ontologies. As of recent, KGs and RDF triple stores (which leverage Sparql queries) have been relaxed into labeled property graphs (graph databases) which do not implement a formal schema or provide for unique (cross-graph) resource identifiers—and other features like federated querying, validation, inference, etc. Labeled graphs utilize more simplistic query languages (i.e. Gremlin graph traversal language).

Some very fascinating deep learning algorithms have been designed to enable graph embedding on knowledge graphs, including the Relational Graph Convolutional Network (R-GCN) implemented by Amazon’s DGL-KE library and available via AWS Neptune ML. Given the multi-relational structure of knowledge graphs, the R-GCN graph accumulates activations across relations in the embedding process. I will cover a few of these algorithms in a future post…

Techniques exploiting deep learning on KGs will become more critical as enterprises become pressed to represent/develop knowledge layers across/between their organizations—integrating human-generated content and semantic layers on top of various enterprise technologies and APIs. These systems will provide natural human interfaces (i.e. question-answering), which will understand both human context and intent.